Want to make people rage quit and call you a virgin?
 
 

Game Basics

I will summarize the important aspects of the graphwar tutorial.
 
See http://www.graphwar.com/tutorial.html – [graphwar.com]  for the graphwar full tutorial.
 
 
If you are comfortable with calculus this guide is not for you.
 
If you are not this guide is for you.
 
 
I recommend starting out to only play in the Y mode.
 
Y’ and Y” are harder to visualize and are calculus related. As well as I will not have any tips for them in this guide.
 
 

Pitfall 1

 
 

 
(fig 2 http://www.graphwar.com/tutorial.html) – [graphwar.com] 
 
 
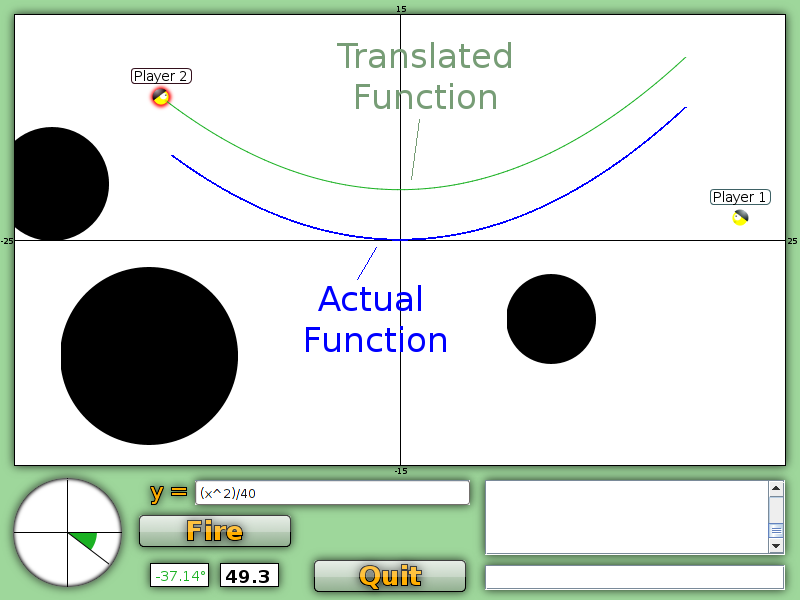
The first big pitfall to understand is where your graph shoots from. It will always shoot from the soldier who’s turn it is.
 
 
That said these graphs will graph the same thing in the game:
 
x+5
 
x+1000
 
x-100
 
 
Why?
 
 
Your line must pass through your soldier. The constant value will not move your graph up and down. That said another way to look at it is whatever your function is moves up and down automatically to perfectly cross that soldier.
 
 

Pitfall 2

 
Your team will always be left of the y-axis. This means any functions you write starts in the negative numbers.
 
 
Square roots for instance will cause issues.
 
Square roots of negative numbers are imaginary and can not be graphed.
 
This will cause your line to instantly exploded, as well as other errors
 
 

Pitfall 3

 
PEMDAS.
 
 
Order of operations applies.
 
 
x/5x is not 1/5.
 
It would resolve to x^2 / 5
 
 
The easiest way is to use parentheses to control order of operations.
 
 
ex 1.
 
x/5x = x^2 / 5
 
(x)/(5x) = 1/5
 
 
ex 2.
 
2x+1x = 3x
 
2(x+1)x = 2x^2 +2x
 
 
ex 3.
 
x+1/x-1 = x-1+1/x
 
(x+1)/(x-1) = (x+1)/(x-1)
 
 
 

How to manipulate formulas

Learning how to manipulate formulas is a major aspect of Algebra.
 
In this section I will go over how to manipulate your formulas for graphwar.
 
 
The basic manipulation will be translation and scaling.
 
Let us say we have a function f(x)
 
 
There are three variables we can control to change how we aim.
 
 
a*f(bx+c)
 
 

a

 
This will control the vertical scaling.
 
If a>1 it will amplify or heighten your formula.
 
If 0<a<1 it will squish or make your formula smaller.
 
Making a negative will flip the direction up and down.
 
 

 
 
y = -x
 
 

 
 
y = x/10
 
 

b

 
This variable will control horizontal scale.
 
Essentially we are squishing the x-axis and making it smaller or bigger.
 
 

 
 
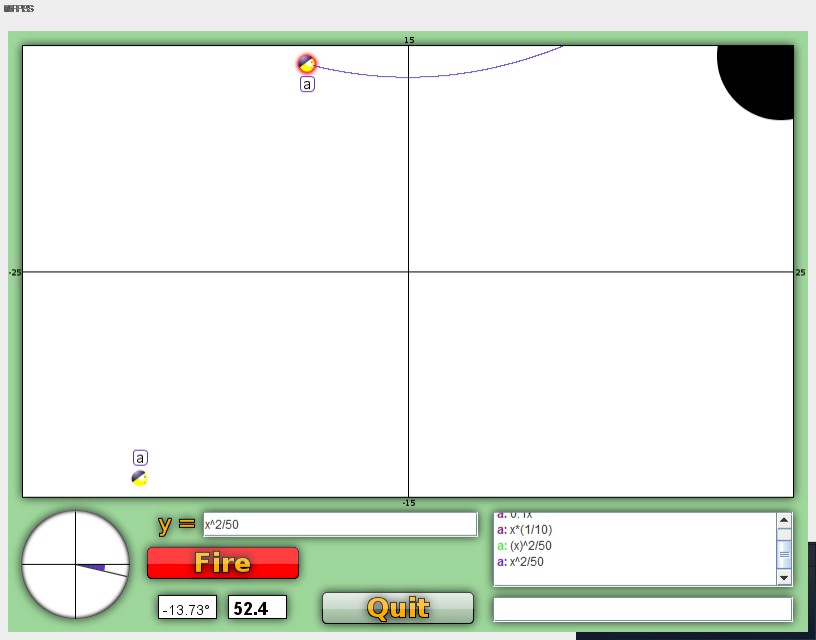
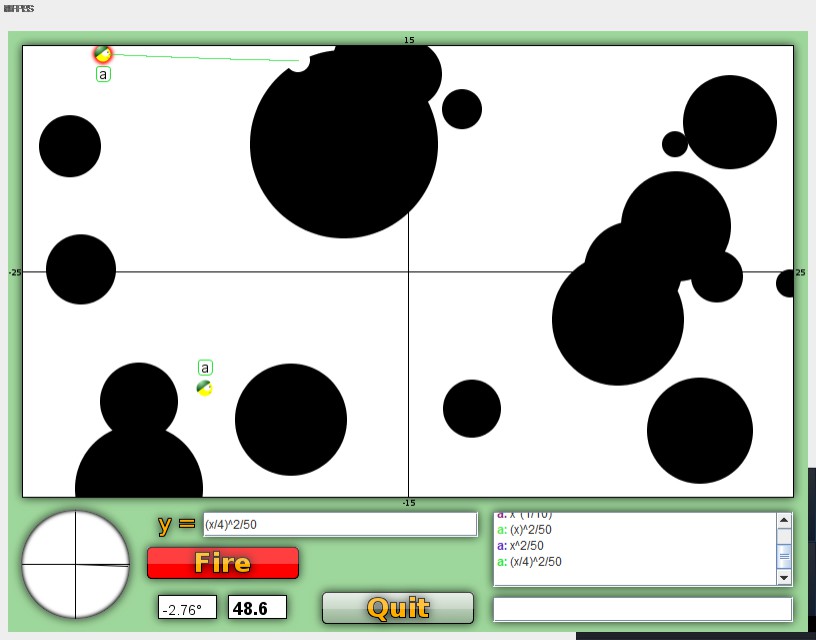
This graph is x^2/50 as our base graph.
 
This is a parabola scaled down to fit on graph war.
 
 

 
 
This graph is where b=1/4. f(x/4) = (x/4)^2/50.
 
As you can see the graph is a lot flatter. Remember the line DOES use the x-value the soldier is at. They are not at zero. But this does mean as far as the function is concerned the x-axis is ranged from -6.25 to 6.25. (25/4)
 
 

 
 
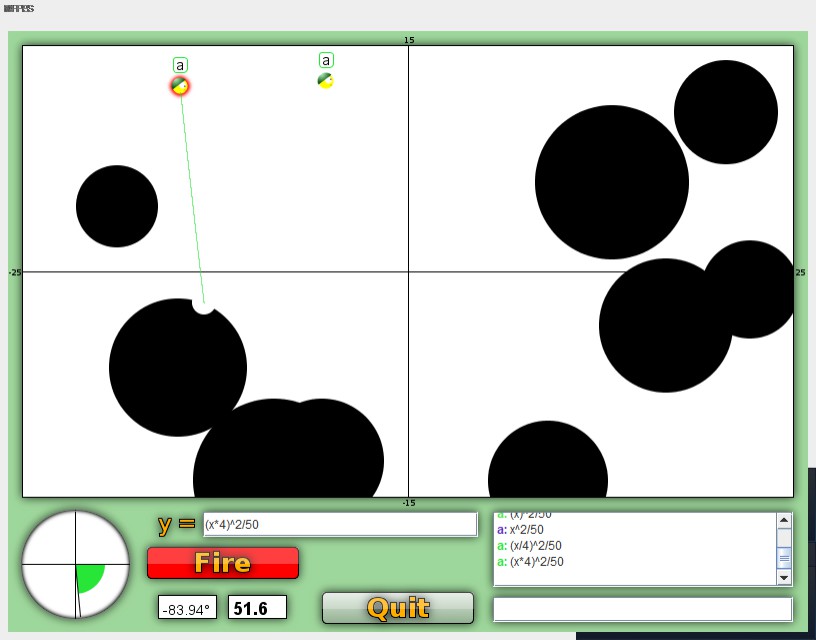
This graph is where b = 4. f(4x) = (4x)^2/50.
 
This graph shoots down really fast because the x-axis is 4 times as large. -100 to 100.
 
Estimating the x-position of the soldier puts it at -13.
 
the difference between -13 and -11 is 15.36. This means this function will very quickly span the entire y-axis.
 
 

c

 
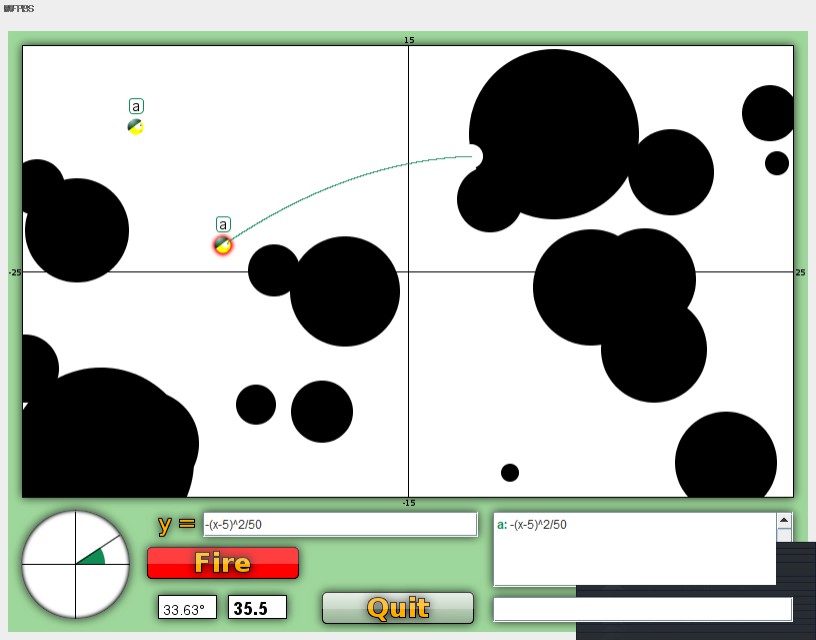
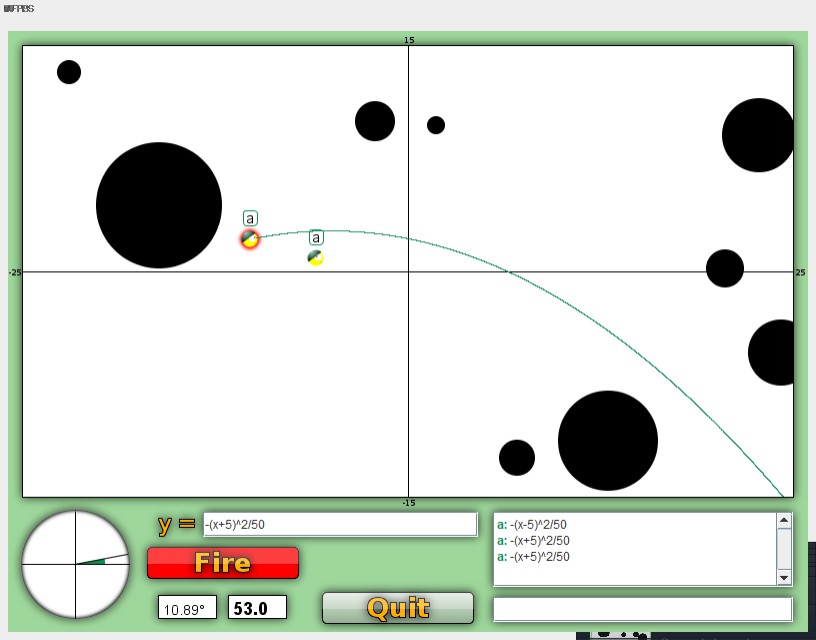
I would argue this is the most important variable to mess around with for functions that are more than just x. This variable is like moving the origin and can help you aim the best.
 
 

 
 

 
 
We can see from these two screenshots by looking at the peak:
 
when c is positive the graph moves left.
 
when c is negative the graph moves right.
 
 
 

Well how does that help me?

The secret is to use formulas that don’t care about the x value of your soldier!
 
 
The two best formula’s I have found are 2^x and tanh(x) and combining them!
 
 
It is hard to aim a parabala when you don’t know your x position.
 
As well as sine and cosine will move weird depending on their b and c values.
 
 
if our function is exponential we can slowly adjust a,b,c and the base to go right and up or down to hit a target.
 
 

 
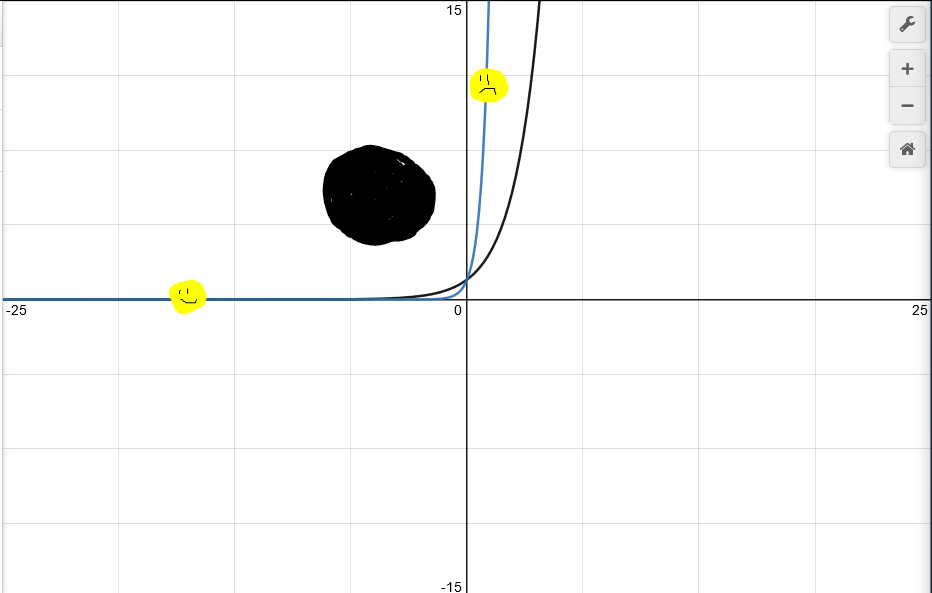
The black line is 2^x and the blue line is 10^x.
 
 
I have found this to be a very common situation. You need to aim around an obstacle.
 
x^2 would work, but they are difficult to aim.
 
 
No matter the x value of your soldier on that graph it will form the same line.
 
You only need to worry about the y value of your soldier as it moves the entire graph up and down.
 
 
Your enemy is further to the right?
 
Well adjust C!
 
 

 
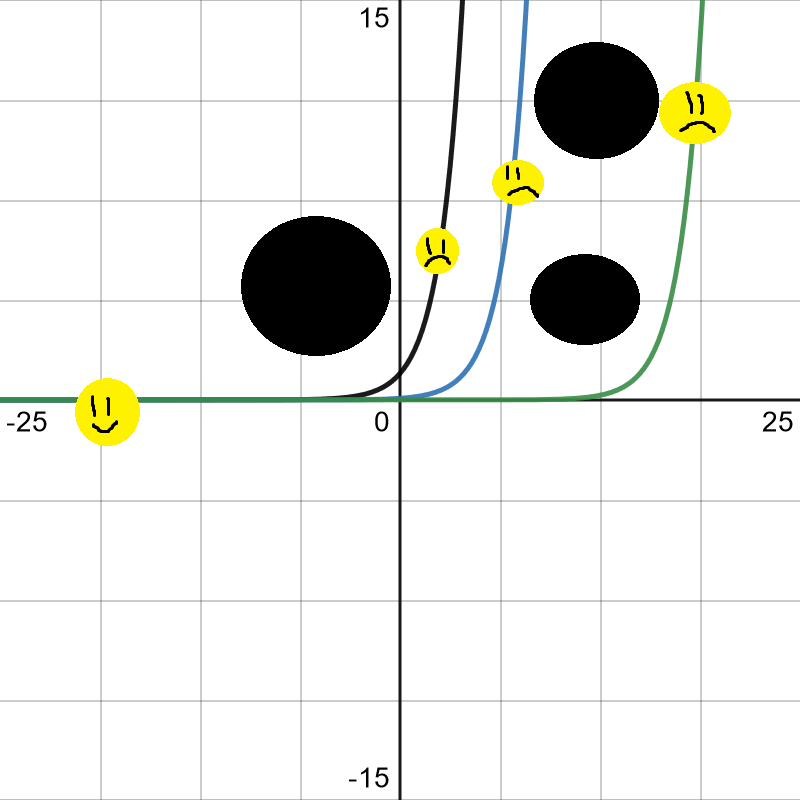
2^(x+c)
 
Black c = 0
 
Blue c = -4
 
Green c = -15
 
 
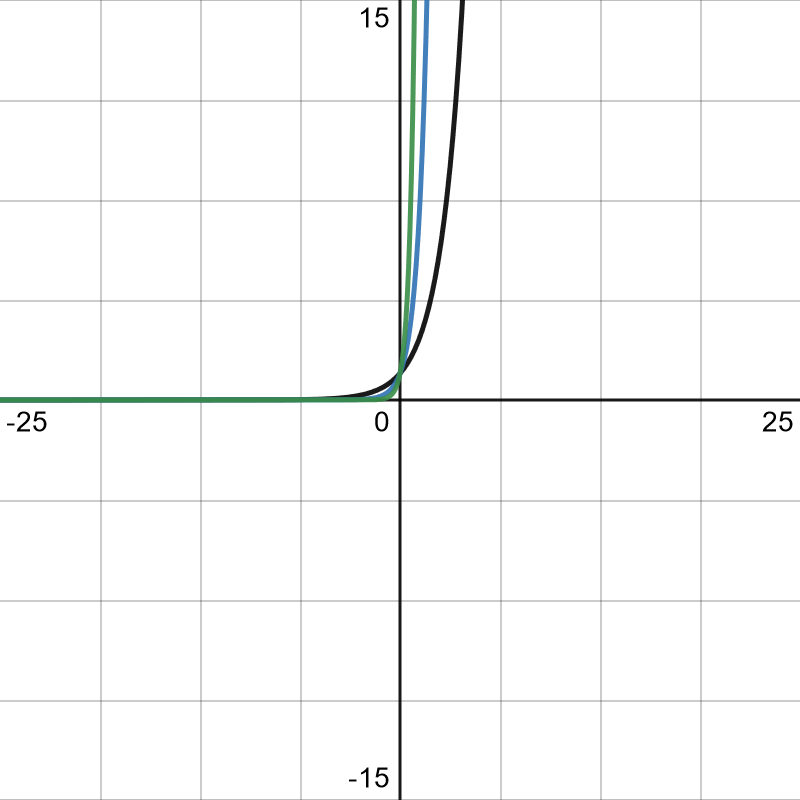
Sometimes 2^x is still a little curvy and you need it to get into a tight space.
 
Increasing the base, 2, to a higher number increases how much of a right angle it is.
 
 

 
Black = 2^x
 
Blue = 5^x
 
Green = 20^x
 
 
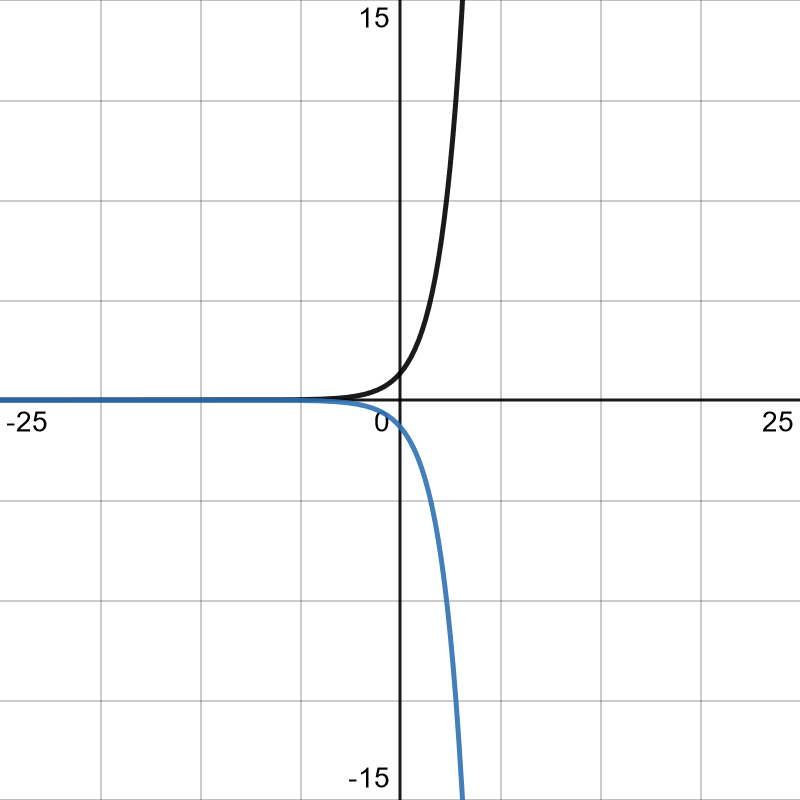
Now what if you need to shoot downwards?
 
Just slap on a – and your formula shoots down!
 
 

 
Black = 2^x
 
Blue = -2^x
 
 
Even between different soldiers the the shape will stay the same shape, just moved up or down.
 
 

What should I put c as?

 
In the case of the formula’s I have listed we adjust c to be an estimate of our enemy soldiers’ x position minus a bit and turned negative.
 
 
Visually halve the x-axis as many times to get an estimate. If they’re in the middle half is 12.5 so a good guess for c would be -11.5.
 
 
12.5 -1 = 11.5
 
11.5 negative is -11.5!
 
 
 

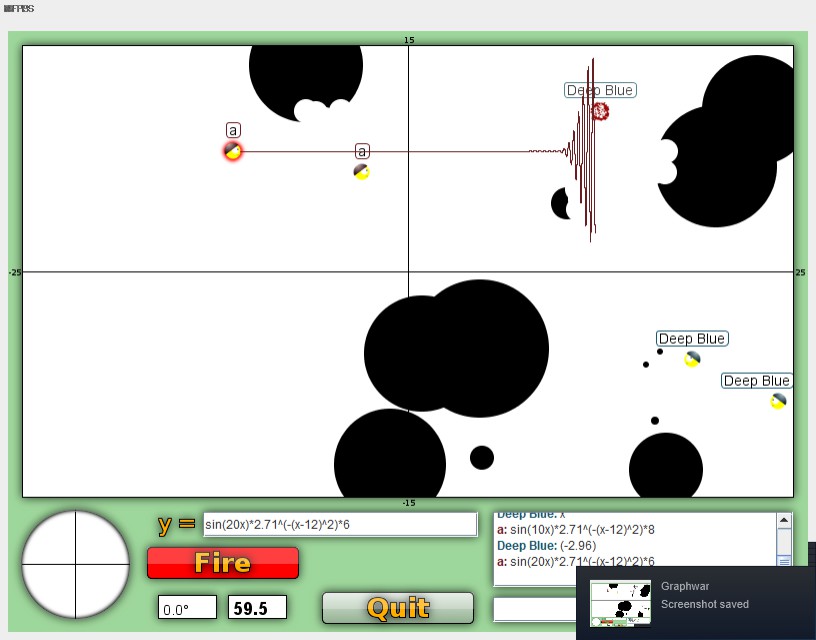
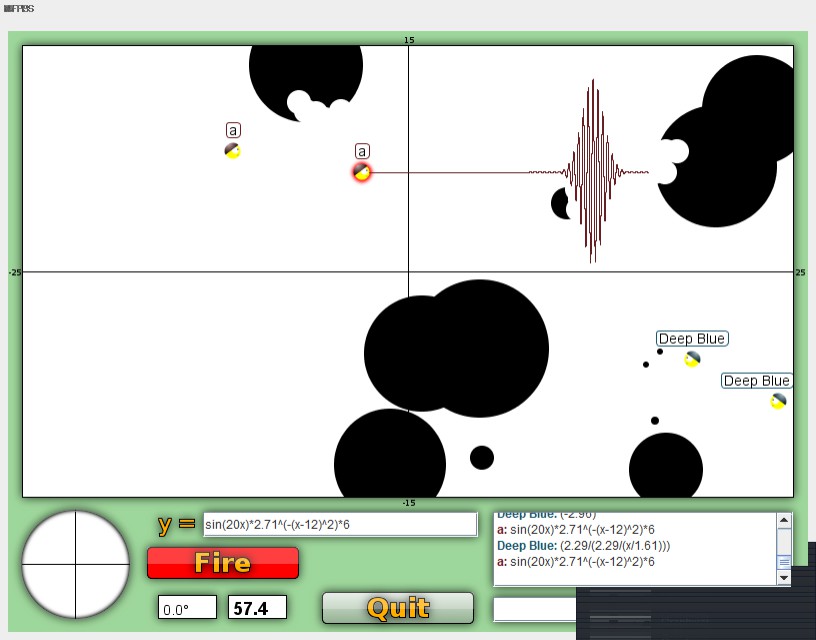
My Favorite Combinations

So far from my recent games my favorite combination has been these 3 formulas.
 
 
ab^(x+c) + sin(40x)*de^(x+f).
 
 
Especially against groups of people in large open areas.
 
 

 
(1/5)*2^((x-2)/3)+sin(40x)*(1/2)*2^(x/2.5-4)
 
 
This formula runs really slow in game but it provides a great area wipe. Easily taking down an open group of soldiers. This one does require a bit of tweaking but is satisfying when it hit.
 
 

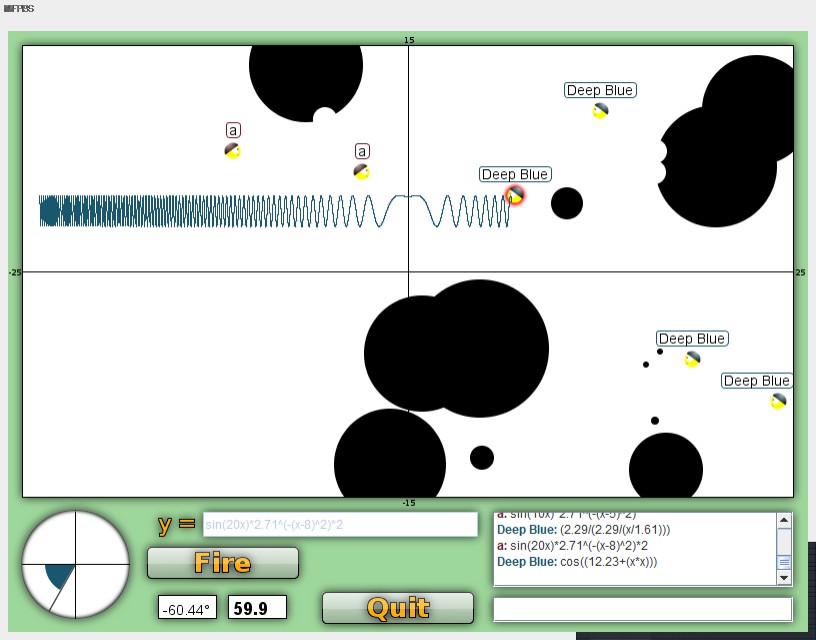
Standard Deviation and Sine

 
 
Another fun combination when they’re on a straight line, in a group, or you’re unsure what exact angle is the basic standard deviation formula and sine.
 
 
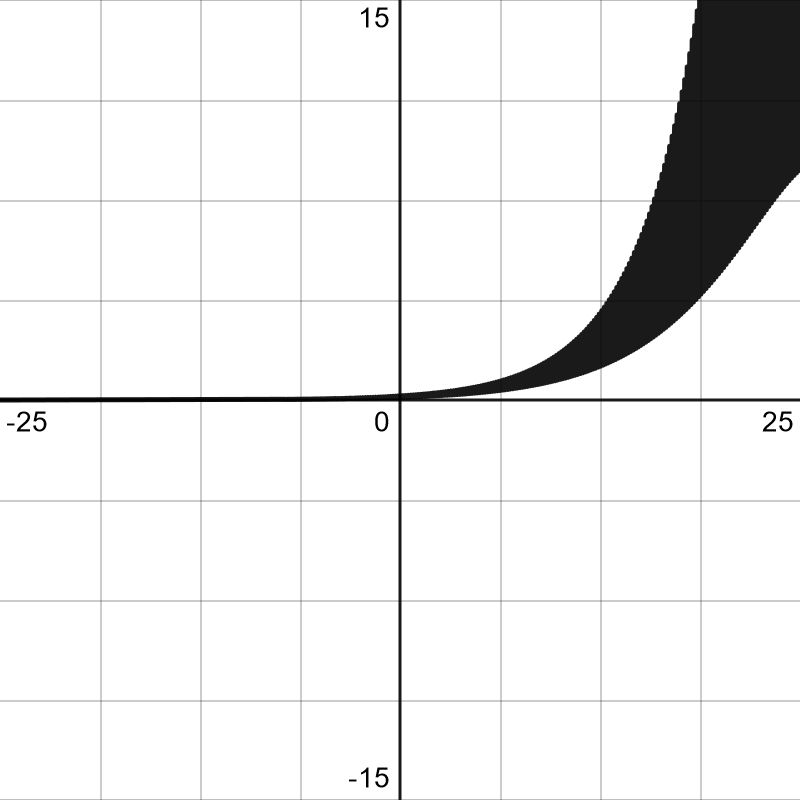
a*e^(-(x+c)^2*sin(20x)
 
 

 
 

 
 
As I mentioned before we use a,b, and c in our function af(bx+c) and specific functions to ignore the x position of our soldier. From both soldiers the action happens relative to c and only the height changes between soldiers.
 
 
In the case of this function the bot ran. We can see that using just sin, x^2, or etc can be difficult to aim because they rely heavily on the x position of the soldier. If they were slightly to the left or right that function would of been a wipe. Their x position put their cosine function at a peak. Lowering the entire function.
 
 

 
 

tanh

 
A personal favorite math function of mine for game design is tanh. Sadly graphwar does not have hyperbolic trig functions so we have to write it out in its entirety.
 
 
tanh(x) = (e^(x)-e^(-x))/(e^(x)+e^(-x))
 
 
and
 
 
tanh(x+c) = (e^(x+c)-e^(-(x+c)))/(e^(x+c)+e^(-(x+c)))
 
 
5*tanh(x-4) = 5*(e^(x-4)-e^(-(x-4)))/(e^(x-4)+e^(-(x-4)))
 
 

 
 
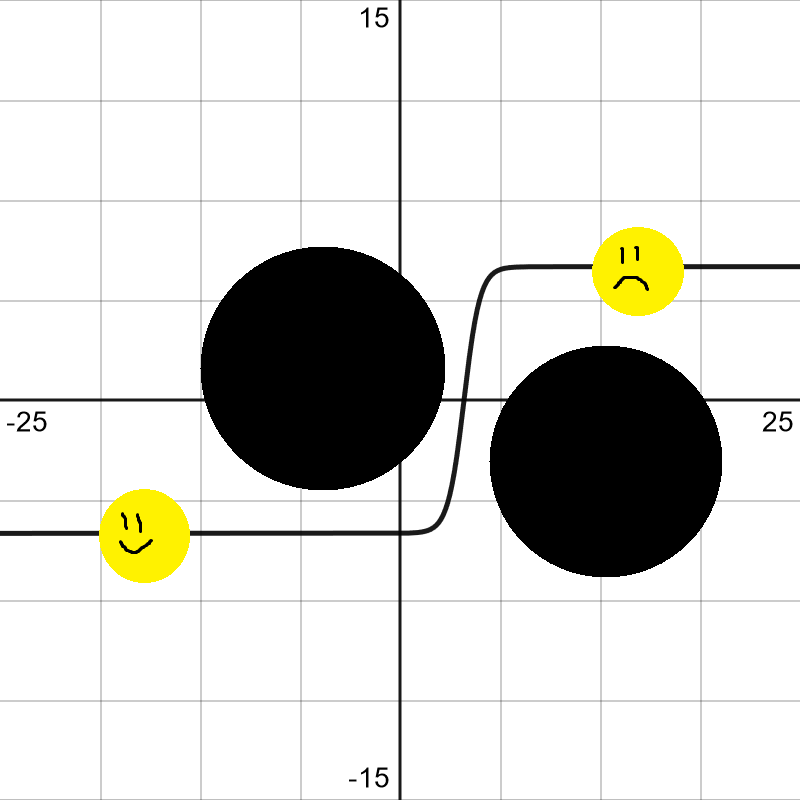
I would argue this is the hardest to aim of these three but is super useful in some really difficult tight spots. What other function would you recommend to even go around the spheres? You could dig yourself through but depending on how deep it is you may leave yourself wide open! Or take forever.
 
 
 

Conclusion

These may not be the best formulas but they sure are flashy and when everyone uses simple algebra and copy and pastes without understanding you now know better and adjust better.
 
 
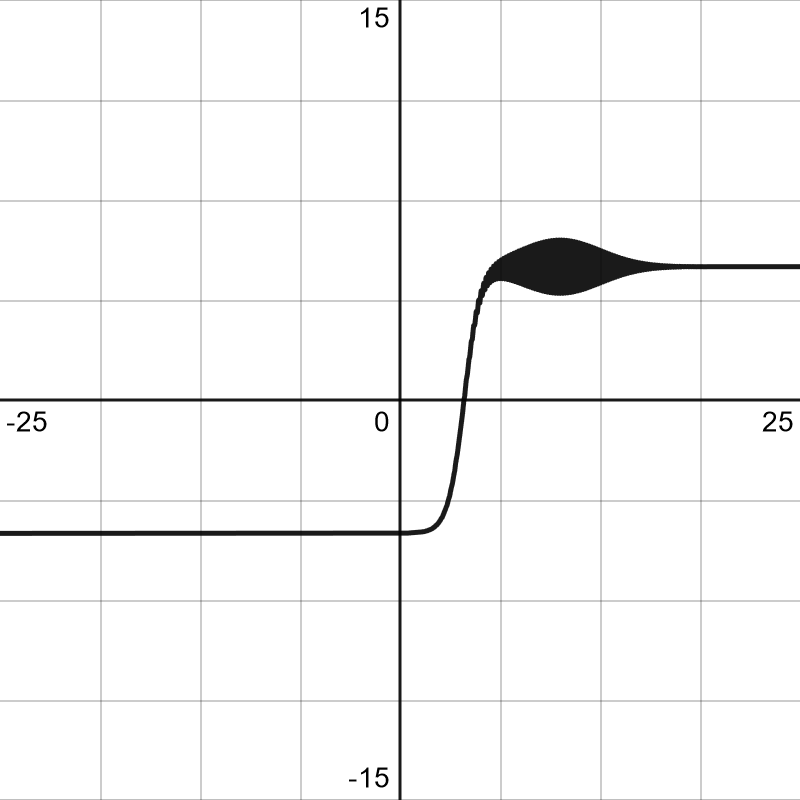
Best of all the last three can be EASILY combined to create some powerful combos.
 
 
5*tanh(x-4)+sin(40x)*2^(-((x-10)/3)^2)
 
 

 
 

 
 
Hope you enjoy the Guide about Graphwar – Useful Formulas & Game Basics, if you think we should add extra information or forget something, please let us know via comment below, and we will do our best to fix or update as soon as possible!