
Welcome to (CRUMB – How to build a full-adder and a 4-bit ripple). This tutorial will demonstrate how to modify a half-adder to produce a full-adder and a 4-bit ripple adder.
Overview
This guide will reuse the half adder from my previous guide.
I will make the half-adder a full-adder. To make a 4-bit ripple carry, duplicate the full-adder.
Contents:
- Modify the half-adder to full adder
- Logic diagram for full-adder and 1-bitfull-adder
- Adder for Ripple
- Conclusion
*Notes – This guide requires understanding the K-map and the half adder.
Abbreviations:
Cin = Carry in
Cout = Carryout
FA = Full-adder
HA = Half-adder
Modify the half-adder to full adder
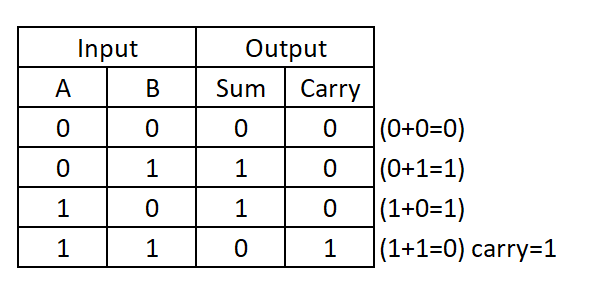
First, we must get the truth table from the previous guide. Below is the truth table for the half-adder. As you can see, the truth table only contains 2 inputs A14Y A and) and 2 outputs A14Y Sum and Carry e17Y.
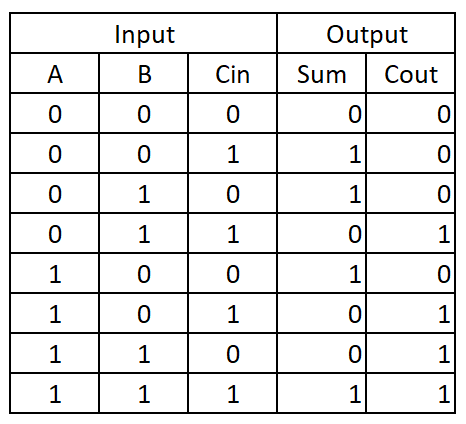
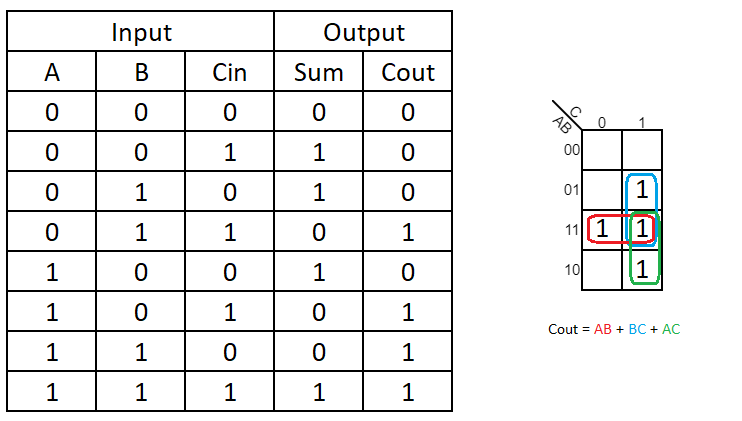
However, a full adder has 3 inputs(A, B & Cin) and 2 outputs(Sum and Cout). We need another truth table to complete the full adder. Below is the truth table for a FA.
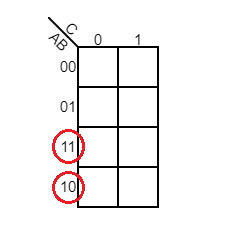
Next, we will need to find the boolean expression for the Sum and Cout a FA. To solve this problem, we can use a 3-variable (B, Cin) Kmap.
This is an empty 3-variable Kmap. When creating the 3/4 variables Kmap, please be aware of the red circle.
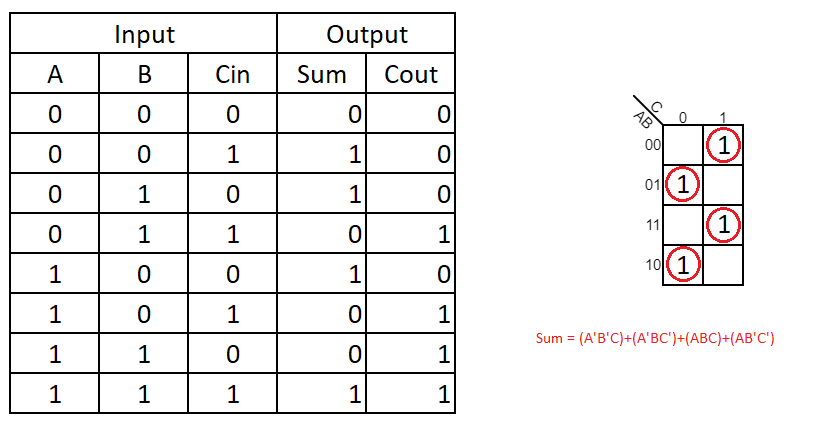
Sum
The boolean expression for Sum output is
This is the tricky part. We need to simplify the process by applying laws and theorems in boolean algebra.
Step 1: We remove the A and A’
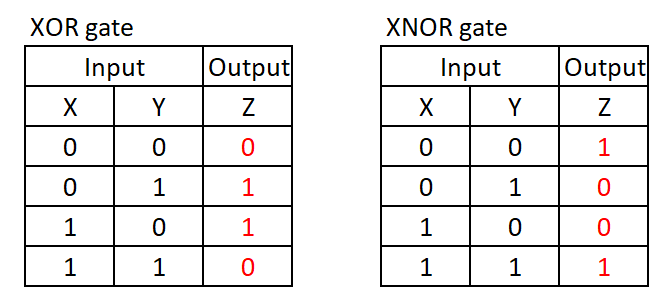
*Important rule (XOR gate): E Y = E’Y + EY’
After removing and A and A’ variables, you can again see the familiar terms (+XY’), which is exclusive-OR (XOR). So X Y = (X’Y+XY’. We can also replace B’C + B’C’ with B’C.
*Important rule (): XY = (XY’ =)’ = EY+ X’Y
Another interesting fact is that if you invert the output of the XOR gate, you get the XNOR gate. We can also replace BC + B’C” to (BC)’
The Sum expression can be simplified.
Sum = A B C
Cout
Cout’s boolean expression is
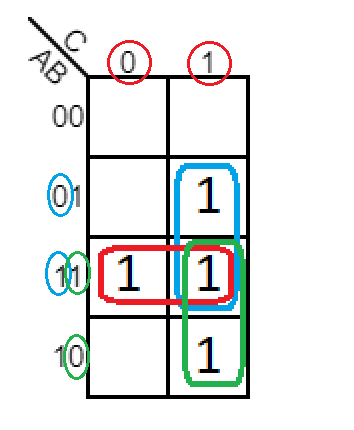
Kmap allows you to circle 1,2,4,8 and 16 slots (, assuming up to 4 variables). As you can see, I circled 2 slots three times.
*Note: Always circle as many slots as possible. The simpler the term, the more slots you circle.
How do I get AB, AC, and BC?
After we have circled the terms in Kmap, we need to verify that (A.B.C.) has both 1 and 0 circled. As shown in the image below, both 0 (or 1) of C is circled in the red circle. We can ignore C and only focus on A and B. In this case, A=1, B=1, so it’s AB. The same concept applies to the blue and green circles.
So Cout = AB + AC+ BC
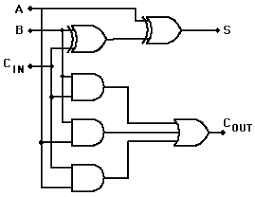
Logic diagram of Full Adder and 1-bit Full Adder
The boolean expression Sum and Carry out from the FA is, therefore a boolean expression.
Sum = A B Cin
Cout = AB + AC + BC
The logic diagram is now complete.
Source:
http://hyperphysics.phy-astr.gsu.edu/hbase/Electronic/fulladd.html – [gsu.edu]
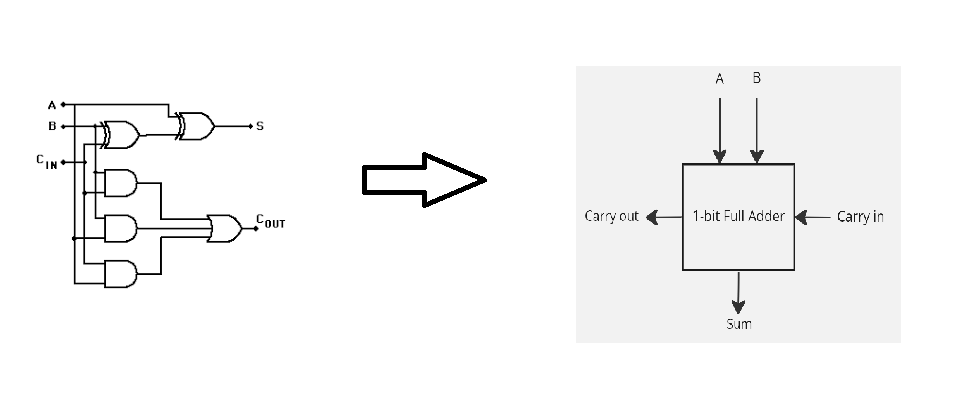
The FA can be simplified into a 1-bit FA diagram.
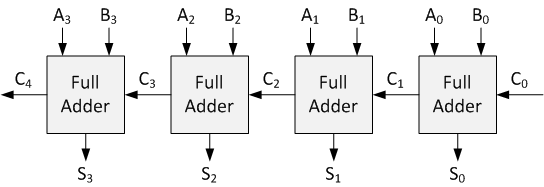
Ripple Carry Adder
The Cout can be connected to the Cin of each bit FA to make it a 4-bit FA. This is also known as the ripple carry adder.
Source:
https://nandland.com/ripple-carry-adder/ – [nandland.com]
To add these 2 numbers, we only need to supply 4-bit inputs A and B (A3A2A1A0. The result will be 5 bits (CoutS3S2S1S0 –
Conclusion
This guide may seem a bit difficult to beginners. These are some tips to help you get started.
- To see a better explanation and demonstration, go to youtube and search YouTube for vids
- Leave a comment to let us know how we can help you
- To get more familiar with electronics, you can look for beginner circuits.
I hope you enjoy this guide. Let me know if I can help you. =)
*Note: At the moment, there is no plan to adder/subtractor with ripple carry adder. This requires an understanding of the signed and unsigned binary numbers and the 1’s 2’s complement. This would require many explanations. If you are interested, you could look for materials to convert your 4-bit adder/subtractor to a 4-bit adder/subtractor. It is easy to do. =)
Thanks.
This is all about CRUMB – How to build a full-adder and a 4-bit ripple; I hope you enjoy reading the Guide! If you feel like we should add more information or we forget/mistake, please let us know via commenting below, and thanks! See you soon!
- All CRUMB Posts List


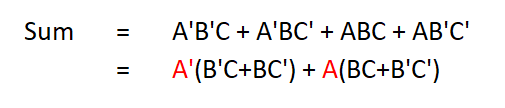
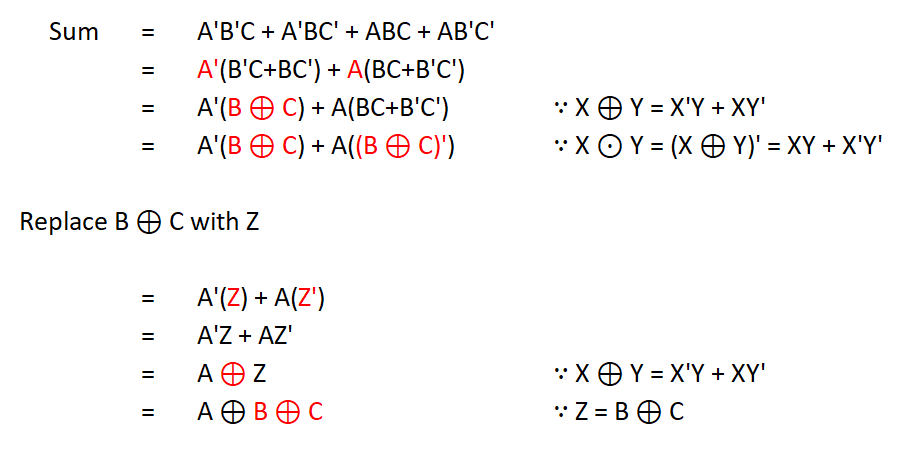
Leave a Reply